Note about
earlier versions
of this talk
|
The Royal Philosophical Society of Glasgow: 31st October, 1990
Maskelyne on Schiehallion
Mr Chairman, ladies and gentlemen,
I thank you for the honour you have done me in inviting me to address your distinguished Society. The invitation your President communicated was not in general, but in fairly specific, terms - it would be appreciated, he suggested, if I would talk about the experiment carried out on the Perthshire mountain Schiehallion in 1774, by the Rev Nevil David Maskelyne, Astronomer Royal to his Majesty King George the Third.
And the President suggested that I endeavour "to exhibit the experiment in a fairly broad context". Earlier this year your Kelvin lecturer, in his pre-ambulatory remarks, referred to the ‘scientific revolution’ associated with the names of Copernicus, Galileo and Newton. Those associated with the Schiehallion experiment certainly saw themselves as participants in that stream of scientific advance, though I think they would have reacted against the term revolution. They refer frequently to Newton in their publications anent this experiment, and they're quite positive in claiming that their results should strengthen belief in the correctness of Newton's hypothesis concerning gravitation.
But let's go back to Copernicus - to 1543, in fact, when he published his great book On the Revolutions of the Heavenly Orbs which embedded in a rational geometry the hypothesis - not original to him - that the Earth and the rest of the planets revolve round the sun: and from that vantage point of 1543 let's recall, briefly, why Copernicus should advance such a hypothesis.
For many millennia, men had observed the sky, and from 743 BC on we have a chronology - much of it accurate to the exact day - based on the observation of solar and lunar eclipses. The sky was observed to feature distinguishable classes of objects. The Sun was unique - but, like all the rest it went round the earth. Most of the sky is occupied by the fixed stars - luminous objects which like holes punched in an opaque shell remained stationary relative to one another, while the whole shell - apparently centred on the earth - rotated, on an axis passing through the earth, a little more rapidly than the Sun. Another set of noctilucent bodies attracted special attention. Five in number, they move relative to the fixed stars, sometimes eastwards, sometimes westwards; but over a long period they all move round the earth, in seemingly capricious tracks.
|
|
|
Various attempts had been made to devise ‘rules’ - nowadays we should probably call them ‘models’ - to describe the apparent motions of the planets as seen from the supposedly stationary earth. Ptolemy, about 115 or 200 AD, had suggested that these complex motions could be represented as the paths of bodies moving with uniform circular motion round imaginary bodies which themselves performed uniform circular motion around the earth. By adjusting the relative radii and rates of rotation, passable (in some sense) approximations to the observed motions could be generated. But what Copernicus pointed out in 1543 was that if the sun was put at the centre of the celestial sphere, and the earth and the planets were assumed to move in circles round the sun with different periods and at different distances, with the earth itself spinning about its polar axis, the apparent rotation of the celestial sphere and the apparent motions of the planets as seen from the earth could all be understood in much simpler terms.
The next major contribution to the kinematical description (i.e. a description in terms of geometry and time, but with no causal explanation) of the planetary motions was provided by the superb observational programme planned and overseen by Tycho Brahe at two observatories in Denmark between 1576 and 1597 - a programme which is believed to have been funded to the extent of about 5 - 10 % of Denmark's g.n.p. at that time by Brahe's patron King Frederick II of Denmark.
Brahe set up two observatories equipped with duplicate sets of the best observational instruments that the technology of the day could provide; the two observatories carried out identical observing programmes, the staffs of each observatory having no knowledge of the results obtained by the other - only Tycho Brahe himself had access to both sets of results. (Imagine trying to do this nowadays in the teeth of "right-to-know" agitators, investigative journalists, and leaky civil servants!) But the result was that both teams of superbly equipped observers were on their mettle all the time. And when Tycho published his results - which were far and away the most accurate thus far obtained - he also attached estimates of error to his observations.
In 1597 Brahe fell out with King Frederick, and left Denmark: he went to Prague where he was appointed Imperial Mathematician. In 1600 he appointed as his assistant Johannes Kepler, then aged 29. Kepler, furnished with Brahe's observational results, was set the problem: what is the orbit of the planet Mars?
It took Kepler almost eight years to arrive at an acceptable solution. He quickly confirmed that a circular orbit with the earth at the centre gave no sort of fit to the data provided by Tycho Brahe. If both Earth and Mars were assumed to circle the Sun the fit to the data was fairly close, but there remained discrepancies which were four times as great as the uncertainties which Brahe had assigned to his observations. Kepler had faith enough in Brahe's figures to regard this as unacceptable. Various ovoidal paths were tried, and found unsuitable. But finally Kepler concluded that the orbits of the planets round the Sun are elliptical orbits, with the Sun, in each case, at one focus of the ellipse. Thus, if the planets speeded up when coming nearer to the Sun and slowed down when receding in accordance with a simple law, the planetary motions could be satisfactorily related to Brahe's observations. This work was published in 1609, and ten years later Kepler added another important discovery to round the work off - if a number of planets revolve in different orbits around a common centre, the squares of the times taken to describe these orbits (that planet's year) are all the same multiple of the cubes of their respective mean distances from the common centre. By this time in his writings Kepler was mixing in astrology and music in ways which we nowadays don't much value; but his three laws of planetary motion paved the way for Newton's work on gravitation.
Newton, born in 1643, enters our story in 1664, in which year he showed that, to constrain the body moving with speed v to move in a circular orbit about a fixed centre, it must be acted on by a force proportional to v 2, and inversely proportional to r.
Then, postulating that this circulating body was a planet, orbiting the Sun and therefore obeying Kepler's Third Law which relates the time taken to complete one orbit to the radius of that orbit, he concluded that there must be a force between Sun and planet inversely proportional to the square of the distance between them. By 1684 he had shown that the inverse square law leads, in general, to elliptic orbits. Arguments of great generality led him then to conclude, further, that this force must be proportional to the mass of each body; so that if S is the mass of the Sun, P the mass of the planet, and PrS the distance of the planet from the Sun, the force of the attraction of either towards the other can be expressed by
P fS proportional to (S times P)/(prS)2
or
P fS = G(SxP)/(PrS)2
Of all the bodies concerned - the Sun, the Earth and the other planets, and the moons of the planets - the body most accessible to us is the Earth.
So - could one weigh the Earth?
Newton asked himself this question, and, in a much-quoted passage, he wrote :
Here reads Principia Vol II, p 570, lines 1-20.
You will notice that Newton regarded his calculations as leading to discouraging predictions regarding the feasibility of both experiments.
But: his prediction about the first effect - the two massive spheres moving together under the influence of their mutual gravitational attraction - was wrong. He seems to have gone wrong in his arithmetic. The time it would take the two 1 ft diameter spheres to move together in empty space as a result of their mutual attraction is not, as Newton calculated it, a month, but five-and-a-half minutes - a difference of four orders of magnitude (the actual ratio is 8,116: 1).
Newton's contemporaries seem to have accepted his conclusion without checking his arithmetic, so this experiment seems to have been not seriously considered for many years.
As to the second possibility - the mountain experiment - Newton's dismissal of this one because the possible plumb-line deviation (he gave it as about two minutes of arc) was too small for actual measurement, seems to have been less seriously received by his astronomer contemporaries. After all, Tycho Brahe had quoted the uncertainties on his measurements as 1-2 arc minutes about 80 years previously. Since then the telescope had been invented, and scientific instrument technology had advanced : astronomers in Newton's day seemed not to have been put off by the alleged improbability of detecting a shift of 1 or 2 arc minutes in the position of a star.
|
|
|
The first significant attempt to do this was due to the French astronomer Bouguer, on Chimborazo, in Peru [now Ecuador]; the year was 1749. The experiment was insufficiently prepared, the instruments were not good enough, the difficulty of working under the harsh conditions on the snow line at an altitude of about 15,000 ft (Chimborazo is about 20,000 ft high, and the Ecuadorian table land, from which it rises, is at about 10,000 ft) had not been prepared for. In fact, though, Bouguer had not really been sent out there by the French Academy to do this experiment - it was done, rather, on the side. The plum-line deviation due to gravity, which Bouguer appears to have detected when he moved his observatory from the south to the west of the mountain, was about 8" of arc; but he himself attached no quantitative significance to the results, and he concluded his account of the experiment with the hope that France or England might contain suitable mountains on which the experiment could be performed under better conditions!
Bouguer had demonstrated the feasibility of the experiment. In 1772 Maskelyne, King George III's Astronomer at Greenwich, proposed that the Royal Society should initiate a repetition of the experiment in England. He had himself made various inquiries, and suggested that the Yorkshire-Lancashire border had a number of suitable hills - one in particular, Whernside, where the contrary attractions of the mountain for a plumb-bob suspended on the N-side, and then on the S-side, might be found; and he mentioned also the possibility of making observations of the contrary deviations of plumb-lines suspended on the north side of Helvellyn and on the south side of Skiddaw, two mountains separated by a tract of low-lying ground. Such an experiment, he reflected, "... would serve to give us a better idea of the total mass of the Earth, and the proportional density of the matter near the surface compared with the mean density of the whole Earth." "The result", he said, "would doubtless do honour to the nation where it was made, and to the society which executed it"!
|
|
|
The Royal Society agreed to a proposal that it despatch a surveyor, a Mr Charles Mason whom they had previously employed on astronomical projects, all the way to Scotland and back, to survey likely-looking mountains, and to select a suitable mountain - ideally it should be a steep-sided cone, or a wedge with its apex ridge running W - E and with steep faces to N and S, and separated from the nearest neighbours to N and S by low land.
Mr Mason selected for them a mountain at "the centre of Scotland", Schiehallion - a wedge, with the summit ridge running nearly W - E, 3547 ft above sea level at its western summit, about 3000 ft at the E-end of the ridge; it presents steep faces to the trench to the N which contains Loch Rannoch and Loch Tummel, and to the deep Gleann Mor to the S. [An approximate altitude for Gleann Mor is 1500 feet, and for the land at the same distance to the north of the ridge is 1600 ft.] So this site was chosen. The Royal Society had available some first-rate astronomical instruments, including a 10' zenith sector, used for observing transits of Venus at St Helena in 1761, other instruments for observing stellar positions, an astronomical clock; and it laid hands on a number of other instruments of comparable quality. Finance turned out not to be a problem, because not all the money put up by the King for a programme of observations of transits of Venus had been spent, and " the bounty of his Majesty, our patron" allowed that unspent balance to be used for this new astronomical experiment.
Maskelyne goes on to record that "The experiment being thus resolved upon, the next thing to be done was to fix on a proper person to carry it into execution. Numerous and interesting as my literary engagements at the Royal Observatory were, I had no thoughts of undertaking this care and labour myself, until the Council of the Royal Society were pleased to do me the honour to think my assistance necessary to ensure the success of so important and delicate an experiment. Their thinking so was sufficient motive with me to encounter whatever difficulties and fatigues might attend operations carried out in so inconvenient and inclement a situation." His Majesty was graciously pleased to approve the requisite leave of absence.
And so, in the spring of 1774 Maskelyne embarked, with his equipment, somewhere in the Greenwich-Chatham area, and set sail - for Perth. At this point it is perhaps appropriate to pause and consider briefly the quality of Maskelyne, and the "difficulties and fatigues" he might expect in "so inconvenient and inclement a situation".
Maskelyne, in his early 40s, was a first-rate astronomical observer, with a taste for good living. The wine bills for his cruise to St Helena in 1761 to observe transits of Venus there have been preserved, and are impressive! But his voyage to St Helena indicates a willingness to face difficulties and fatigues in inconvenient situations - the ships of those days offered little in the way of comfort, poor food, and probably a fairly noxious environment. He was a notable mathematician, and one of the few British mathematicians of his day to be sympathetic towards the new mathematical analysis which was developing in continental Europe and making little headway on this side of the English Channel.
1772, the year in which Maskelyne made his submission for a mountain experiment to the Royal Society, saw Mr and Mrs Walter Scott celebrate the first birthday of their son, Walter. He was the Walter with whom John Buchan was concerned in the great biography which he wrote, and Buchan gives, in his first chapter, a vivid account of the state of Scotland in 1772. In that year Edinburgh was certainly Europe's City of Culture, and perhaps no Scottish city has so well deserved that title since. But outside the cities Scotland was a harsh place. "The land and the people were grievously poor, and North of Forth the Highlands had to face the decadence of their ancient social and economic structure, and in the space of a man's lifetime adapt themselves to the change from a medieval to a modern society."
The clan system, which had been the basis of the social system, and of law and order, had been shattered after the failure of the Jacobite rebellions. "She [Scotland] was conscious of being poverty-stricken and backward... A friendly visitor ... might find something to patronise and praise, but the common traveller's tale was only of a bleak land, vile weather, dirty farms and shabby stone towns ... The dislike of Scotland ... was a universal feeling in the south. It was returned in kind..."
So Maskelyne may well have felt that an expedition to Scotland was a pretty unattractive proposition. He was going to be living - for as long as it took to complete a massive programme of observations - high up on the sides of a mountain whose name, "in the Erse language", he was told, meant "constant storm". One wonders why - if that were justified - they chose it as the site for two observatories!
|
|
|

By the beginning of July 1774, by which time Maskelyne's presence had been reported in Scots Magazine, his locally recruited labour force had levelled a platform on the S face of Schiehallion at a height of about 2000 ft, built a bothy for the astronomer, and a modest tower to house and protect his zenith telescope. He spent six weeks there, making in all 169 observations of the zenith distances of 39 stars.
The telescope swung on a horizontal axis, which pointed east and west. So the movement of the telescope was in the plane of the Meridian - the local N-S plane - and the telescope could be angled to point a few degrees N or S of the vertical. Stars were observed as they crossed this N-S vertical plane, and their deviations from the vertical direction indicated by the plumb-line were noted. After six weeks at the Southern Observatory, Maskelyne transferred to a similarly prepared platform on the N-face of the mountain, at a height of about 2300 feet; this platform can still be seen, and is clearly identifiable [this is no longer true]. Local labour was hired to carry all the equipment up over the ridge from the South to the North platform. There he established himself and, a week after closing down the southern observatory, he was ready to resume his observing programme. He then had a fortnight of bad weather, until about the 5th of September. The observing programme at the North observatory - where 168 observations were made on 37 stars, occupied him until October 24th, a period of seven weeks. In all, he was on the mountain for 16 1/2 weeks. In the absence of the gravitational effects of the mountain, the observations of any star at the S and N stations should have differed by 42.94'', that being the difference in latitude between the two stations. But the differences observed averaged 54.6''. The difference - taken as 11.6'', was attributed to the gravitational displacement of the plumb-bobs by the mountain.
|
|
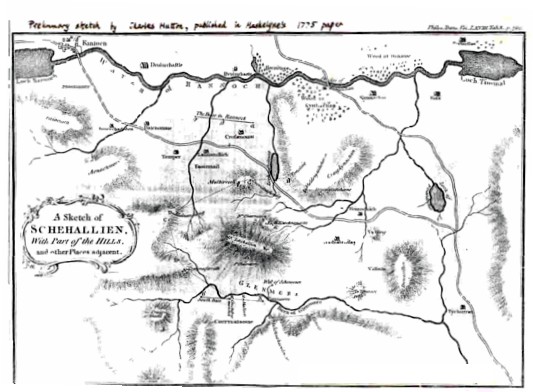
I said a moment ago that the difference in latitude between the two stations was 42.94'' (corresponding to a horizontal distance of 0.81 mi or 1430 yards). There were no maps from which such information could be read. So there was another programme of work to be done - to survey the mountain, and so acquire detailed knowledge of its 3-dimensional form. Responsibility for this was assigned to a distinguished surveyor and mathematician, Dr Charles Hutton FRS. He, with skilled assistance from Mr Reuben Borrow, of the staff of the Royal Greenwich Observatory, established two base lines, one on the flat ground between Lochs Rannoch and Tummel, and one in Gleann Mor. These were related to one another by a survey carried round the base of Schiehallion, to determine the relative positions and alignments of the base-lines. Cairns were built at each end of the summit range, and their positions and heights relative to the base-lines were determined, as were those of the South and North positions of the zenith telescope. That much of the surveying programme took from July until mid-November, being so prolonged by foul weather. Indeed, Maskelyne tells us that "... all the people of the country agreed it was the worst season that had ever been known." That has quite a contemporary sound to it!
Whatever Maskelyne's ideas about Scotland may have been before he came north, he took a good impression back with him - in spite of the weather: "all the gentlemen of the neighbourhood often paid me visits on the hill and gave me the fullest conviction that their country is with justice celebrated for its hospitality and attention to strangers". In addition to these local visitors he was visited by academics from the universities of Glasgow, Edinburgh and Aberdeen, and by senior civil servants from these cities.
The information Maskelyne took back to Greenwich with him consisted of his own astronomical observations, the results of the survey thus far; also measurements had been made of the density of the outcropping rock. This enabled him to calculate the angle between the verticals at the two stations, to subtract from that the latitude difference, and so to arrive at the figure of 11.6'' which I've already mentioned; and in addition, to estimate the volume of the mountain, the position of the centre of gravity, and - assuming the density of the whole mountain to be that of the rock outcrops - to estimate its mass.
If one were to assume that the mean density of the earth were the same as that assumed for Schiehallion - that is to say, 2.5 times the density of water - then, knowing the positions of the observatories and the positions of the centres of gravity of Schiehallion and of the Earth, it's an easy matter to calculate what plumb-line deviations would have resulted: the answer is 20.9'' of arc. But the observed angle was 11.6''. This means that the mean density of the Earth is greater than 2.5 in the ratio of 20.9 : 11.6. This implies a mean density for the earth of 4.5 relative to water. Hence, knowing the volume of the Earth one can calculate its mass. From that one can arrive at mean densities and masses for the Sun and the other planets, for which only ratios of densities had been known hitherto.
Maskelyne reported on the experiment and on these conclusions in a long paper presented to the Royal Society in 1775, and published in the Philosophical Transactions for that year. In a sense this was an interim report. But the detailed survey of the mountain and surroundings out to a distance of about two-and-a-half miles, occupied Charles Hutton and Reuben Borrow for another two seasons. It led to no change in the figure deduced for the mean density of the earth, but it was a striking achievement; Hutton devised novel and very ingenious procedures in both mensuration and computation, and he ended up presenting the results of the survey in a very conveniently visual form - as a contour map. This was an original invention by Hutton. Hutton's paper - "An account of the calculating made from the survey and measures taken at Schiehallion... etc." is in Phil. Trans. for 1778, and runs to 100 pages.
|
|
|
In 1798 the Hon. Henry Cavendish published - also in Phil. Trans. - an account of his success in performing the "other experiment", the measurement of the mutual attraction of small suspended masses. This was in essence a successful realisation of the experiment Newton had speculated about, to measure the mutual attraction of two 1 ft diameter spheres. In this case one knows by immediate measurement the masses of the two interacting bodies, and one knows their distance apart. So if one measures the force between them, one can calculate the value of the universal gravitational constant G. And from this one can then derive the mean density of the earth - for which Cavendish found the result 5.448 which is clearly at variance with Maskelyne's value.
At this point we get into a rather detailed and technical area. One of the major and obvious uncertainties attending a mountain experiment is that the inner rock structure of the mountain is difficult to determine. In 1811 Professor John Playfair (Professor of Natural Philosophy in Edinburgh) carried out a lithological survey to try to determine the nature, direction, and extent of the rock strata in and around Schiehallion; on the basis of his results he revised upwards Maskelyne's figure for the earth's mean density to somewhere in the range of 4.56 to 4.87, still a long way below Cavendish's value. Charles Hutton, in a very testy paper, asserted that (i) he hadn't been given his fair share of the credit for his contribution to what is, even to this day, called "the Maskelyne experiment"; (ii) Cavendish's experiment is in principle inferior to the mountain experiment (which, in terms of the knowledge then available, it isn't!); and (iii) Cavendish did his arithmetic wrong (which he didn't!). And Hutton ended up saying that probably the best deduction from the Schiehallion experiment is that the mean density of the Earth is 4.95 times that of water.
In the years since Hutton's outburst in 1821 there have been many repetitions of both the Maskelyne and the Cavendish experiments, and other, different, experiments have been devised and performed. But it seems to be the case that mountain experiments tend to give too low a value for the mean density, and this is almost certainly due to difficulties in allowing for the gravitational effects of very distant earth-masses. For instance, in a mountain experiment carried out on Arthur's Seat in Edinburgh in 1856, where the survey was extended out to radii of about 15 to 20 miles, it was shown that these distant regions contributed significantly to the observed effect, and that the Schiehallion survey was certainly too limited.
Nowadays there are other and better ways of achieving the goals that Maskelyne had set himself, and gravitational surveys are generally made by geologists, in the quest for information about the sub-surface geological structure. This does not in any way detract from the importance of what Maskelyne, Hutton, and their helpers achieved in their day; and it's appropriate to end this discourse with the words with which Maskelyne concluded his great paper of 1775:
"... whatever experiments of this kind be made hereafter, let it always be gratefully remembered that the world is indebted for the first satisfactory one to the learned zeal of the Royal Society, supported by the munificence of George the Third."
Mr Chairman, ladies and gentlemen, thank you for your attention.
|
|
|
This text is copyright ©R M Sillitto 1990 - 2003
Photo of Schiehallion from Carn Mairg ©H G Sillitto 1971
Photo of Schiehallion from south east ©Allister Combe, 2007
All other photos ©M J Smyth 1962
In 1999 ownership of the eastern part of the mountain passed to
the John Muir Trust. You can find out a lot more about it on
the Trust's website, and buy superb postcards and
pictures from their on-line shop or from the
John Muir Birthplace in Dunbar.
|